【吴恩达深度学习系列第二课第一周笔记】
现在开始记录第二课程的笔记。会慢慢更新的。
关键概念:
不同类型的初始化会导致不同的结果
认识复杂神经网络初始化的重要性
识别 train / dev / test 集之间的差异
诊断模型中的偏差和方差问题
学习何时以及如何使用规范化方法
理解深度学习中的实验问题
使用梯度检查来验证反向传播实现的正确性
正确设置训练集,验证集(开发集)测试集
在机器学习小数据量时代即当你的数据集在100,1000,10000的时候,可以采用60%:20%:20%的比例来,即用60%的数据来训练模型,20%的数据来评估不同你不同的模型,最后用20%的数据集来评估选定模型的性能。
但是当数量达到百万级别时,我们就可能不在需要这么高的比例来划分出验证集。因为验证集的目的就是用来快速验证不同的算法之间的差别,所以可能不再不要这么多的数据作为验证集。举个例子,当我们有一百万的数据时,可能只需要一万条数据来验证就行了。同样的,最后的测试集也是如此。所以最终的比例就是98%:1%:1%。对于数据量过百万的情况,可能就是99.5%:0.25%:0.25%.
训练集和测试集分布不匹配
比如说你有个应用,通过用户上传图片,然后告诉用户这张图片是不是猫咪。相比较而言,你的训练集都是从网上下载下来的高分辨率图片,并且构图精巧。而用户上传的图片可能分辨率就不是很高,并且更加随意。这个时候你的训练集和测试集的分布就不一样了。对此,吴老师的建议是确保分布相同,具体会在后面的课程提到。
偏差和方差以及偏差方差权衡
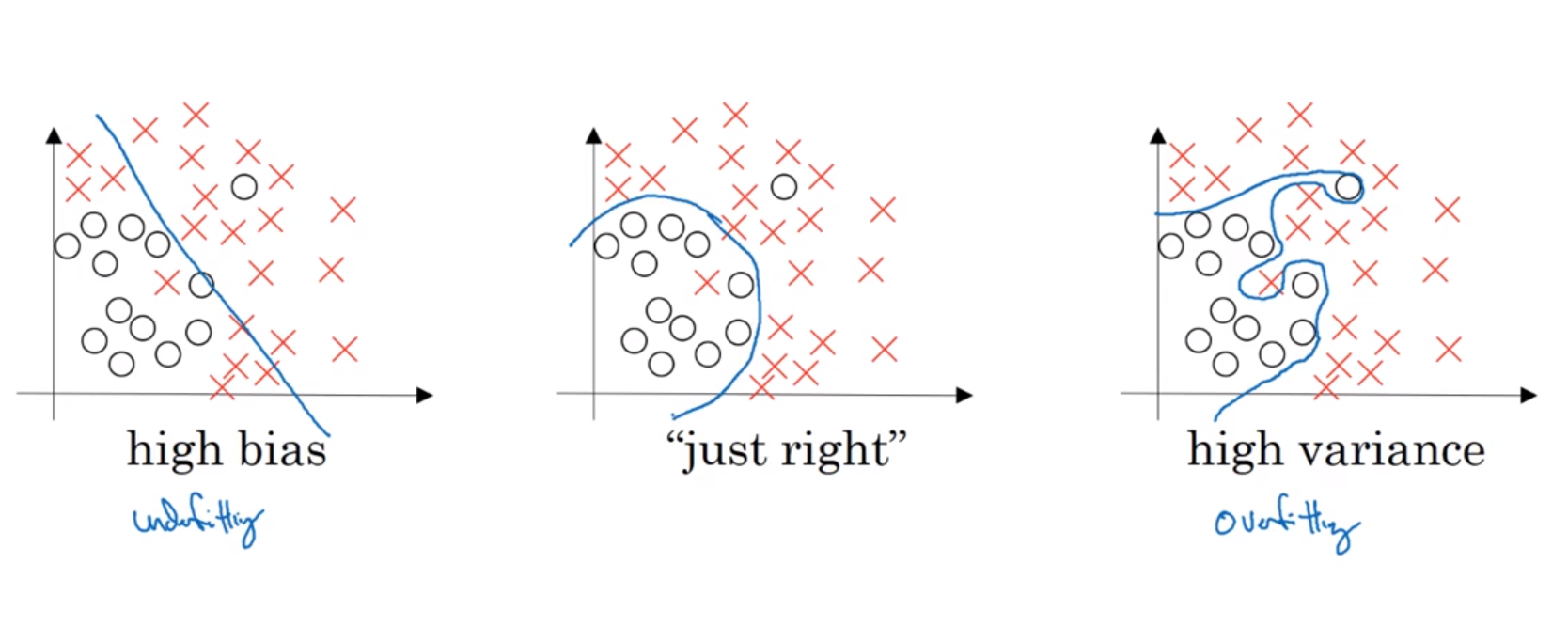
对于偏差和方差问题应该都会有大致了解了。比如高偏差对应欠拟合,高方差对应了过拟合。如图所示:
接下来看看如何分析偏差和方差:
假设你有个识别猫咪的分类器,得到了不同的误差集合:

- 当训练集误差是第一列时,可以看到在训练集上误差很小,但是在验证集上误差很大,说明过拟合了。
- 当训练集为第二列时,可以看到在训练集和验证集上的表现都不是很好,说明该模型在训练集是欠拟合,而在验证集上表现也符合该预测
- 当训练集为第三列时,训练集和验证集的表现都不行,并且验证集的表现比训练集差很多。说明该模型不仅存在高偏差的问题,并且还存在高方差的问题。也就是说该分类器在总体上是欠拟合的,但是在部分数据上又表现出过拟合的问题。
- 第四列则是开发人员很希望看到的,就是在训练集和验证集上的误差都很小,说明是适拟合的情况。
机器学习的基本方法
当训练好你的网络,首先应该看看是否存在高偏差的问题:
- 如果存在,则尝试减少,例如使用更大的网络,训练的更久一点等等这些方法
- 如果不存在,则看看有没有高方差的问题。如果存在,尝试获得更多的数据,或者正则化
尝试上面的方法,直到找到低偏差,低方差的网络。
正则化
正则化的定义
如果你的NN发生了高偏差,一般可以采用正则化来尝试解决问题。获取更多数据也是解决高方差问题的一个很可靠的方法 ,但你并不是总能获取到更多的训练数据 ,或者获取更多数据的代价太大 。但使用正则化通常有助于防止过拟合 并降低网络的误差。
逻辑回归模型
在逻辑回归中,你会尝试最小化代价函数J ,该代价函数定义为 :每一个训练样本的预测的损失之和 其中w和b是 逻辑回归的参数 ,因此w是一个x维的参数向量 b是一个实数,要为逻辑回归正则化 你需要加上这个lambda 它称为正则化参数。正则项被定义为:
这里的也可以叫做w的范数,也被称作L2正则化。与此同时,有另一种正则化叫做L1正则化,如下:
如果使用L1正则化,w最后会变得稀疏,这意味着w矢量中有很多0 。有些人认为这有助于压缩模型 ,因为有一部分参数是0 只需较少的内存来存储模型,然而在实践中发现 通过L1正则化让模型变得稀疏,带来的收效甚微 所以我觉得至少在压缩模型的目标上 它的作用不大 。在训练网络时,L2正则化使用得频繁得多。(注意:==在python中,lambda是保留关键字,所以用lambd代替==)。在上面发现,正则化参数时,并没有将b包含进来,实际上你可以这样做,但通常会把它省略掉。因为你可以看一下你的参数w往往是一个非常高维的参数矢量,尤其是在发生高方差问题的情况下 可能w有非常多的参数,你没能很好地拟合所有的参数,而b只是单个数字,几乎所有的参数都集中在w中 而不是b中,即使你加上了最后这一项,实际上也不会起到太大的作用。因为b只是大量参数中的一个参数。
神经网络
在神经网络中,你的正则项定义如下:
这个矩阵的范数称为矩阵的弗罗贝尼乌斯范数,使用角标F标记。由于线性代数中某些神秘的技术原因这不叫矩阵的L2范数而是称为矩阵的弗罗贝尼乌斯范数,它表示矩阵中元素的平方和。
为什么正则化可以解决过拟合
看个例子
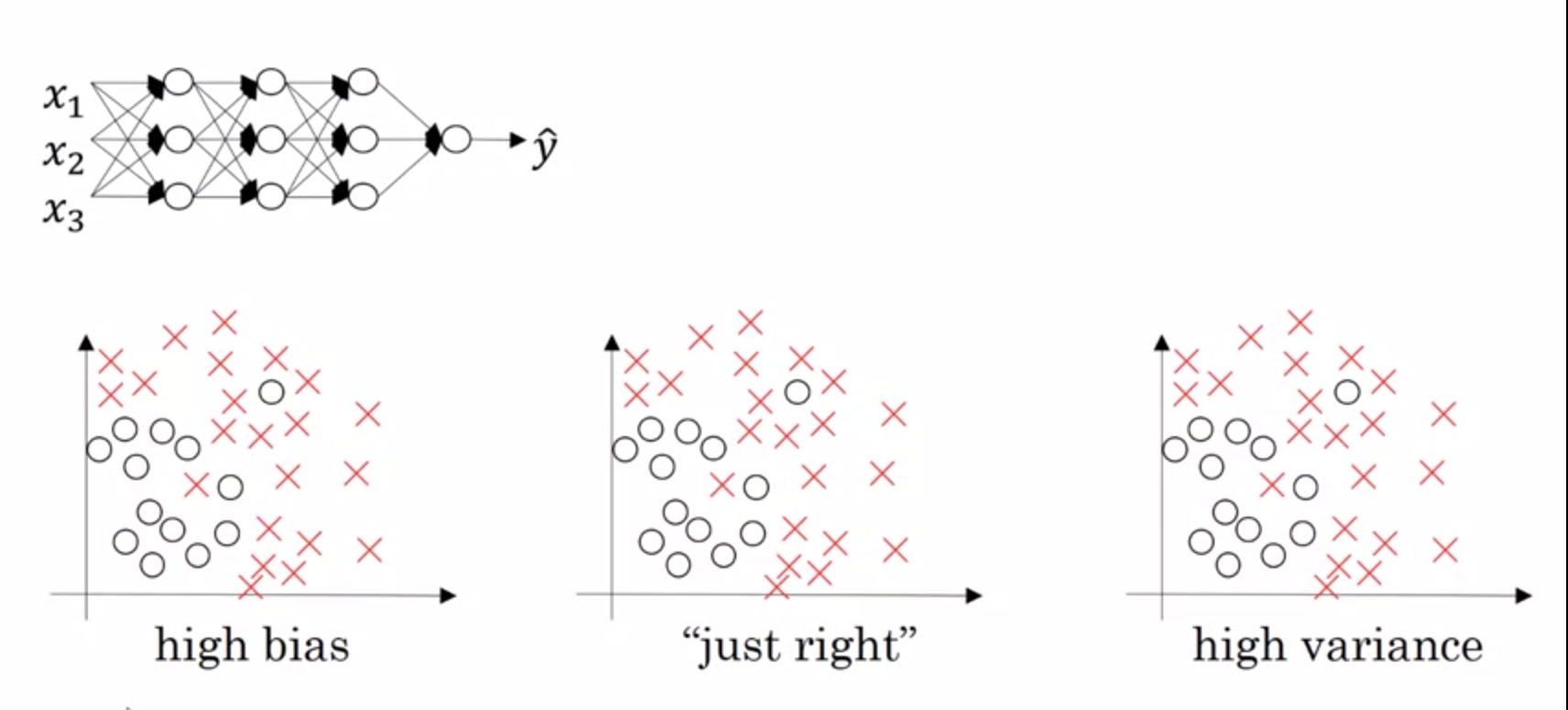
在高方差的情况下,当你把lambda的值设置的很大,就相当于把W设置为非常接近0的值。也就是说隐藏层的影响会很小,因此这个网络最终就相当于逻辑回归模型。但是lambda存在一个中间值,可以把高偏差这种情况变成”just right”。
另一种常见正则化——随机失活正则化(丢弃法 dropout)
这种方法就是在你的网络上,遍历每个节点。然后以一定的概率丢弃节点,最后形成一个小的多的网络,在这上面进行反向传播
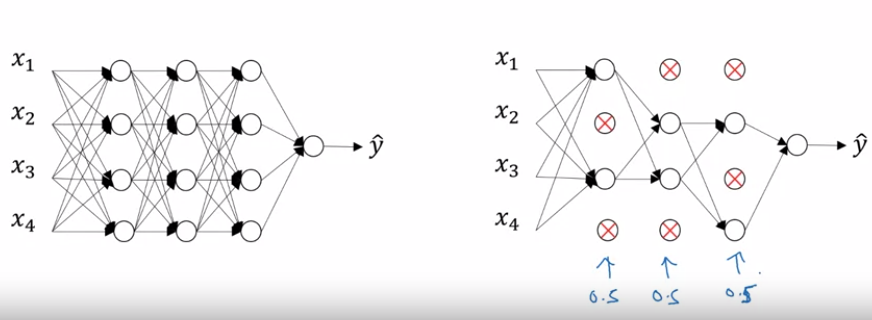
下面看个栗子,如何用代码实现丢弃法,(反向随机失活)
首先定义一个阈值keep.prob = 0.8,然后随机生成一个新的矩阵 d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep.prob。在这个矩阵中每个元素有80%的概率为1,20%的概率为0(严格来说,这是一个True和False的矩阵,但是在python中这样是可行的)。 a3 = np.multiply(a3,d3)或者 a3 *= d3。这样就可以实现随机丢弃了。但是到这还没结束,需要以下这一步骤 a3 /= keep.prob。来解释一下它。假设a3层有50个隐藏单元,所以a3的维数为50x1,如果是矢量化运算则为50 x m。每个单元有80%的概率保留,20%的概率丢弃,这意味着平均下来有10个单元被丢弃。而 。所以的期望值会减少20%,e为了不让的期望不被减少,就让除以0.8,这样就可以修正期望值。这就是反向随机失活。需要注意的是,在每次迭代训练中,每次丢弃的都应该不同,而不是一直丢弃相同的单元。
理解随机失活
使用随机失活后,好像使用一个小的网络,就可以实现正则化。那么是为什么是这样呢?因为对于某个隐藏单元来说,它的每个输入都可能被丢弃,所以会尽可能的分散权重,不让某个输入的权重过大。这样就有了收缩权重以及防止过拟合的功能。准确的来讲,随机失活应该被看做一种自适应而不是正则化。
在网络上使用这张方法时,不同的隐藏层可以使用 不同的阈值,比如某些层你认为不会过拟合,则将阈值设为1,。但是这么做的代价是超参数过多导致运行较慢。另一种方法是在某些隐藏层设定相同的阈值,然后其它层不设置。
其他正则化技术
数据集增广(data augmentation)
我们知道,增加训练集,可以解决过拟合问题。所以在现有数据集的情况下,我们可以对图片进行一些处理,;来新增数据,比如对图片进行旋转,放大,裁剪等等。这样我们会得到新的数据集。这也是解决过拟合的一种手段。
早终止法(early stopping)
这种方法就是画出在训练集和开发集上代价函数关于迭代次数的图像。在开发集的代价函数最小时提前终止训练。
优化网络
归一化
首先如何归一化呢?先算出输入x的平均值,再全体减去均值。然后令σ^2等于 Xi**2之和除以m ,最后在同除以σ^2。同时也要对测试集,开发集进行归一化。
为什么要归一化
因为不用的特征的范围是不同的,有的范围从0-1,有的0-100,这就会导致权重比例不平衡,并且会导致梯度下降很慢。当归一化之后,数据范围都是相近的,就不会出现上述情况了。
梯度消失和梯度爆炸
当训练神经网络时我们会遇到一个问题,尤其是当训练层数非常多的神经网络时。这个问题就是梯度的消失和爆炸 它的意思是当你在训练一个深度神经网络的时候,损失函数的导数或者说斜率有时会变得非常大或者非常小甚至是呈指数级减小,这使训练变得很困难。举个栗子,你的激活函数为线性函数,当你的网络非常深,并且权重矩阵大于1的时候这个时候就会出现梯度爆炸的问题,事实上的最后的预测值是指数级增长的。同样,当权重矩阵的值小于1时,就会出现梯度消失的问题。
如何尽量避免梯度消失和梯度爆炸
- 随机初始化权重矩阵
假设你的激活函数为ReLu,那么可以这样初始化:
如果是tanh:
或者

